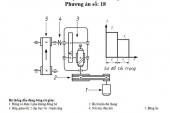
ĐẦU PHÂN ĐỘ KHÔNG CÓ ĐIA CHIA

ĐẦU PHÂN ĐỘ KHÔNG CÓ ĐIA CHIA, thuyết minh ĐẦU PHÂN ĐỘ KHÔNG CÓ ĐIA CHIA, động học ĐẦU PHÂN ĐỘ KHÔNG CÓ ĐIA CHIA

Chương I
TỔNG QUAN VỀ CƠ CẤU VI SAI
I. Hệ thống bánh răng
1. Đại cương
1.1. Công dụng của hệ thống bánh răng

­ Hệ thống bánh răng có thể truyền chuyển động quay với tỉ số truyền lớn. Một cặp bánh răng thường chỉ truyền với tỉ số truyền nhỏ. Nhưng trong thực tế cần phải có những cơ cấu thực hiện tỉ số truyền lớn. Lúc đó cần phải dùng hệ thống nhiều cặp bánh răng.
­ Hệ thồng bánh răng dùng để thay đổi tỉ số truyền. Trong một số máy cần phải thay đổi tộc độ khi làm việc (hộp số trong máy, trong ô tô…).
Trên hình 1.1a là sơ đồ của hộp số. Trục I có 3 bánh răng gắn chặt lên trục. Trục II có 1 khối di trượt gồm 3 bánh răng. Khối này di trượt trên trục II, có thể lần lượt tiếp xúc với 3 bánh răng trên. Chuyển động quay được truyền từ trục I sang trục II với 3 tỉ số truyền khác nhau.
­ Hệ thống bánh răng dùng để thay đổi chiều quay. Khi bánh răng 1 ăn khớp với bánh răng 2 hoặc 2, tỉ số truyền từ trục I đền trục II sẽ đổi dấu.
Vì vậy, nếu trục I có chiều quay nhất định, thì trục II có thể quay 2 chiều,
tuỳ theo vị trì tay gạt A (hình 1.1b).
­ Hệ thống bánh răng dùng để hợp chuyển động và phân tích chuyển động.
1.2. Phân loại hệ thống bánh răng


­ Hệ bánh răng thường (hình 1.1)
Trong hệ bánh răng thường, đường tâm của các trục bánh răng là cố định.
­ Hệ bánh răng ngoại luân: trên  hình 1.2 là hệ bánh răng ngoại luân, đường tâm của trục bánh răng 2 di động quanh tâm O.
Tên của các khâu:  
                                 khâu 1 ­ bánh răng trung tâm.
                                 khâu 2 ­ bánh răng vệ tinh.
                                 khâu C ­ cần.
Hệ bánh răng ngoại luân được chia thành:
+ Hệ thống vi sai:
Hệ thống vi sai là hệ bánh răng ngoại luân, trong đó không có bánh răng ngoại luân nào cả.
Bậc tự do của hệ thống vi sai: cơ cấu hình 3 gồm 3 khâu động, 3 khớp loại 5, 1 khớp loại 4. Vì vậy: W = 3n – (2p5 + p4) =2.
Cơ cấu có thể nhận 2 quy luật chuyển động (2 khâu dẫn). Cơ cấu vi sai có thể hợp 2 chuyển động, hoặc phân tích thành 2 chuyển động thành phần.
+ Hệ thống hành tinh:
Là hệ thống hành tinh trong đó có bánh trung tâm. Cơ cấu trên hình 2 nếu bánh răng 1 cố định,  được hệ thống hành tinh.
Khi đó: n = 2;    P5 = 2
                           P4 = 1
Bậc tự do của cơ cấu hành tinh: W = 1.
+ Hệ thống vi sai kín:


Trong hệ thống vi sai kín có thêm 1 xích truyền động bánh răng khác, nối từ bánh trung tâm này với bánh trung tâm kia hoặc với cần. Xích truyền động này có thể là một hệ bánh răng thường, hoặc 1 hệ bánh răng hành tinh, hoặc 1 hệ hỗn hợp. Như vậy, chuyển động của các bánh trung tâm với cần phụ thuộc lẫn nhau, làm giảm bậc tự do của cơ cấu vi sai. Vì vậy hệ vi sai kín có 1 bậc tự do (hình 1.3). Bánh trung tâm 1 nối với bánh trung tâm 3 bằng hệ thống bánh răng thường 1 – 4 – 4 – 3.
  N =5;              P5 = 5
                         P4 = 4
 Vậy:                W = 1
Thí dụ trên hình 1.4a, các bánh răng 1 và 3 đặt trong các gối đỡ I và III sẽ quay với vận tốc góc  và . Trục quay của hai bánh 1 và 3 nằm trên cùng một đường thẳng (mặc dù giữa 2 bánh răng này không có liên hệ trực tiếp). Cần dẫn C cũng quay quanh trục hình học của các bánh răng 1 và 3 với vận tốc góc  và mang gối đỡ II (gối đỡ di động). Trục của hai bánh răng 2 và 2 quay tự do trong gối đỡ này. Như vậy, chuyển động của bánh răng 2 và 2 gồm 2 chuyển động: quay quanh trục của nó và cùng với cần dẫn C quay quanh trục của các bánh răng 1 và 3.
Chuyển động của các bánh răng 2 và 2 gần giống như chuyển động của các hành tinh, nên cơ cấu được xét là cơ cấu hành tinh. Các cơ cấu bánh răng dù chỉ có trục hình học của một bánh răng di động đều được gọi là cơ cấu hành tinh. Các bánh răng chỉ quay quanh trục cố định trung tâm (bánh răng 1 và 3) là các bánh răng trung tâm, các bánh răng có trục hình học di động (bánh răng 2 và 2) gọi là bánh răng vệ tinh. Trong cơ cấu hành tinh trên có số khâu n = 5, số khớp động loại 5 (các khớp quay) P5=4, số khớp động loại 4 (khớp cao giữa các răng) P4=2. Số bậc tự do của cơ cấu:
               W = 3(n-1) ­ 2 P5    ­ P4
             W = 3(5-1) ­ 2 .4    ­ 2 = 2
Cơ cấu đợc xét có hai bậc tự do nên để có thể xác định được chuyển động của các khâu cơ cấu phải có 2 khâu chủ động. Giả sử cho vận tốc góc của khâu 1và 3 ( và ) ta có thể xác định được vận tốc góc của cần dẫn , hay cho vận tốc góc của 1 khâu và cần dẫn, ta sẽ xác định được vận tố góc của khâu thứ 3. Cơ cấu hành tinh có 2 bậc tự do được gọi là cơ cấu vi sai.



Cơ cấu vi sai được dùng để dẫn động từ 2 nguồn chuyển động độc lập đến cùng một bộ phận làm việc hay để dẫn động từ một động cơ điện hai bộ phận làm việc có vận tốc độc lập nhau. Trong ô tô, cơ cấu hành tinh dùng để truyền chuyển động từ động cơ đến các bánh chủ động. Vấn đề là ở chỗ khi ô tô chạy thẳng trên quãng đường bằng thì vận tốc góc của 2 bánh chủ động bằng nhau, nhưng khi xe chạy trên quãng đường vòng, các vận tốc góc của hai bánh chủ động lại khác nhau. Cơ cấu vi sai làm nhiệm vụ phân phối lại vận tốc giữa hai bánh tùy theo độ cong của đường.
Nếu trong cơ cấu hành tinh có hai bậc tự do cố định 1 bánh răng trung tâm, ta sẽ được một cơ cấu hành tinh đơn giản hay còn gọi là bộ truyền hành tinh (hình1.4-b) và bằng cách lựa chọn số răng thích hợp vận tốc góc giữa bánh răng trung tâm và cần dẫn hết sức khác nhau, do đó bộ truyền hành tinh thường dùng để biến đổi vận tốc trong phạm vi rộng (thường là để giảm tốc) mà vẫn bảo đảm kích thước nhỏ gọn.
2. Động học hệ thống bánh răng
2.1. Hệ thống bánh răng thường
Trên hình 1.5 chuyển động được truyền từ trục I đến trục V qua một hệ thống bánh răng thường. Tỉ số truyền từng cặp bánh răng:           
            
Tỉ số truyền từ trục I đến trục V:
            
                  tích số răng của các bánh bị động
Công thức tổng quát để tính tỉ số truyền của hệ thống bánh răng thường:
                 (1.1)
2.2. Hệ bánh răng ngoại luân
Xét hệ vi sai biễu diễn trên hình 1.2. Chúng ta sẽ tìm hiểu quan hệ vận tốc
giữa các khâu. Có nhiều phương pháp để tìm hiểu quan hệ này. Sau đây sẽ tìm hiểu phương pháp chuyển động tương đối trong chuyển động tương đối với cần C, tức là cho toàn bộ hệ thống quay quanh trục O với vận tốc góc ­; Vận tốc góc của các khâu:
            Khâu1: =
            Khâu2: =
            Cần C: =
Như vậy, trong chuyển động tương đối với cần C, đứng trên cần C quan sát chuyển động, cần C đứng yên, hệ thống bánh răng ngoại luân trở thành hệ thống thường. Sẽ dùng đẳng thức (1.1) để tìm quan hệ vận tốc giữa các khâu. Tỉ số truyền giữa cặp bánh răng 1 và 2 trong chuyển động tương đối với cần C:
                                                                  (1.2)
Hệ thức 1.2 biểu thị quan hệ vận tốc góc giữa các khâu của hệ thống bánh răng ngoại luân.
Như vậy, quan hệ vận tốc góc các khâu trong hệ ngoại luân được xác định bằng cách viết tỉ số truyền của hệ thống trong chuyển tương đối đối với cần C. Trong chuyển động đó, hệ thống ngoại luân trở thành hệ thống thường và có thể sử dụng công thức (1.1) để viết tỉ số truyền.
Đối với hệ thống bánh răng vi sai kín, muốn tìm mối quan hệ vận tốc góc giữa các khâu, có thể lập công thức tỉ số truyền trong hệ thống vi sai hở tương ứng và tỉ số truyền trong xích truyền động nối kín từ bánh răng trung tâm này đối với bánh răng trung tâm kia hoặc với cần.
Ví dụ 1: Cho hệ thống bánh răng như hình 1.6. Xét chuyển động tương đối của hệ thống đối với cần C tức là cho toàn bộ hệ thống quay quanh trục OO với vận tốc góc ­ (với Z2=99,  Z3=101, Z1= Z2=100, ).